Confidence interval measures the level of uncertainty or certainty in the sampling method. They can take several probability limits, the most common being a 95% or 99% confidence level. Confidence interval is carried out using statistical methods, such as t-tests.
Statistic experts use confidence intervals to measure uncertainty in the sample variable. For example, a researcher chooses a different random sample from the same population and calculates the confidence interval.
It aims to see how it can represent the actual value of the population variable. The data collection is different, some breaks include the true population parameters, and others do not.
A confidence Interval is a range of values, limited above and below the average statistical, likely to contain unknown population parameters.
Understanding Confidence Interval
The confidence level refers to the percentage of probability or certainty that the confidence interval will have the actual population parameters when you draw random samples many times.
Or, in everyday language, “We are 99% confident (the level of trust) that most of this sample (confidence interval) contains the actual population parameters.”
The most significant misunderstanding of the confidence interval is that they represent the percentage of data from specific samples between the upper and lower limits.
For example, a person may mistakenly interpret the 99% confidence interval mentioned above from 70 to 78 inches as indicating that 99% of data in random samples are among these numbers.
This is not true, although a separate statistical analysis method exists to make such a determination. Doing so involves identifying the mean and standard deviation of the sample and plotting these numbers on the bell curve.
How to Calculate Confidence Interval
Suppose a group of researchers is studying the heights of high school basketball players. The researchers took a random population sample and set the average size to 74 inches.
The 74-inch average is the point estimate of the population mean. Point estimates are of limited use because they do not reveal the uncertainties associated with the forecast.
It would be best if you had a better sense of how far this 74-inch sample mean is from the population mean. What needs to be added is the degree of uncertainty within this single sample.
Confidence intervals provide more information than point estimates.
The Researchers can arrive at an upper and lower bound with an accurate mean of 95%. They used the sample mean and standard deviation, assuming a normal distribution represented by the bell curve. It established 95% Confidence Intervals.
Assume the interval is between 72 inches and 76 inches. Suppose researchers take 100 random samples from the entire population of high school basketball players. In that case, the average should fall between 72 and 76 inches across the 95 samples.
If researchers want greater confidence, they can extend the interval up to 99% confidence.
Doing so always creates a broader range, leaving room for a more significant number of samples. Suppose they set the 99% confidence interval between 70 and 78 inches. In that case, they can expect 99 out of 100 samples evaluated to contain an average value between these numbers.
On the other hand, a 90% confidence level implies that we expect 90% of the estimated interval to include the population parameter and so on.
Confidence Intervals Formula
The formula to find Confidence Interval is:
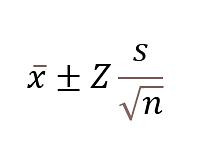
- X bar is the sample mean.
- Z is the number of standard deviations from the sample mean.
- S is the standard deviation in the sample.
- n is the size of the sample.
The value after the ± symbol is known as the margin of error.
Question: In a tree, there are hundreds of mangoes. You randomly choose 40 mangoes with a mean of 80 and a standard deviation of 4.3. Determine that the mangoes are big enough.
Solution:
Mean = 80
Standard deviation = 4.3
Number of observations = 40
Take the confidence level as 95%. Therefore the value of Z = 1.9
Substituting the value in the formula, we get
= 80 ± 1.960 × [ 4.3 / √40 ]
= 80 ± 1.960 × [ 4.3 / 6.32]
= 80 ± 1.960 × 0.6803
= 80 ± 1.33
The margin of error is 1.33
All the hundreds of mangoes are likely to be in the range of 78.67 and 81.33.
The Z-Value
The Z-value is a measure of how many standard deviations away a data point is from the sample mean. It is commonly used in statistics to determine the likelihood of a specific outcome occurring.
A Z-value of 1.96 corresponds to a 95% confidence level, while a Z-value of 2.576 corresponds to a 99% confidence level.
The sign of the Z-value indicates whether the data point is above or below the mean, with positive values indicating it is above the mean and negative values indicating it is below the mean. A Z-value of zero indicates that the data point is equal to the mean.
What Can We do with Confidence Interval?
The Confidence Interval is the range of values, bounded above, and below the statistical mean, likely to contain the unknown population parameter.
Confidence refers to the percentage probability or certainty that the Confidence Interval will have the proper population parameter when you draw a random sample multiple times.
How Does it Use?
Statisticians use the Confidence Interval to measure uncertainty in a sample variable.
For example, a researcher selects different samples randomly from the same population and calculates a Confidence Interval for each piece to see how it represents the actual value of a population variable.
The resulting data sets are different in that some intervals include accurate population parameters and others do not.
Confidence Interval Misconception
The biggest misconception about Confidence Intervals is that they represent the percentage of data from a given sample that falls between the upper and lower bounds.
In other words, it would be wrong to assume that a 99% Confidence Interval means that 99% of the data in a random sample falls between these limits. That means one can be 99% sure that the range will contain the population means.
The T-Test
Confidence intervals are performed using statistical methods, such as the t-test. The t-test is an inferential statistic used to determine whether there is a significant difference between the means of two groups, which may be related to certain features.
Calculating the t-test requires three fundamental data values. They include the difference between the mean values of each data set (called the mean difference), the standard deviation of each group, and the sum of the data values of each group.
Conclusion
A confidence interval is a method used to estimate population parameters based on a sample using specific statistical methods within a certain range.
The confidence level measures the confidence of a confidence interval test. The margin of error is needed to determine the tolerance limit of the confidence interval.
The larger the sample size, the smaller the margin of error and the more accurate the resulting confidence interval.
There are 4 commonly used confidence intervals:
- Confidence interval for the mean of a population
- Confidence interval for the difference in the means of the two populations
- Confidence intervals for differences in population proportions
- Confidence interval for the mean difference of two population proportions
The confidence interval is a researcher’s effort in carrying out various hypothesis testing or other predictions to produce a value that is believed to have parameters in it.
