We encounter many Covariance and Correlation when we do regression analysis or experimental designs. Well, these two analyzes are the most well-known and often used by practitioners like me.
By definition, correlation is a term describing the strength of the relationship between two random variables linearly. Meanwhile, covariance is a term that shows how much the two random variables change together.
Covariance
Covariance is a statistical term defined as a systematic relationship between a pair of random variables in which a change in one variable is offset by an equivalent change in the other variable.
The Covariance can take any value between -∞ to +∞, where a negative value indicates a negative relationship. In contrast, a positive value represents a positive relationship.
Further, it ensures a linear relationship between variables. Therefore, when the value is zero, it indicates no relationship. Moreover, when the two variables’ observations are equal, the Covariance will be zero.
In Covariance, when we change the unit of observation on one or both variables, there is no change in the strength of the relationship between the two variables but the value of the covariance changes.
Covariance Value
It can range from -∞ to +∞, with a negative value indicating a negative relationship and a positive value indicating a positive relationship. The greater the covariance, the more reliant the relationship.
Positive covariance denotes a direct relationship and is represented by a positive number, while a negative number denotes negative covariance, which indicates an inverse relationship between the two variables.
Covariance is useful for defining the type of relationship between variables, but it can be difficult to interpret the magnitude. The formula for covariance can be represented as: Σ(X) and Σ(Y) is the expected values of the variables
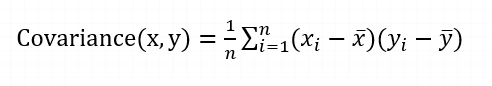
Where,
- xi = data value of x
- yi = data value of y
- x̄ = mean of x
- ȳ = mean of y
- N = number of data values.
Application of Covariance
Covariance is a statistical measure that is used to determine the relationship between two variables. It is commonly used in a variety of applications, including:
- Simulating systems with multiple correlated variables. One way to do this is through Cholesky decomposition, which is a method for decomposing a positive semi-definite matrix into the product of a lower triangular matrix and its transpose. A covariance matrix can be used to determine the Cholesky decomposition because it is positive semi-definite.
- Dimensionality reduction. Covariance matrices are also used in principal component analysis (PCA) to reduce the dimensions of large data sets. PCA is a method for identifying patterns in data and expressing the data in a new coordinate system that captures the most important information. An eigen decomposition is applied to the covariance matrix to perform PCA.
In short, covariance is a useful tool for understanding the relationship between variables, and it has a wide range of applications in statistics and other fields such as data analysis, computer science and engineering.
Correlation
Correlation is a measure in statistics determining the degree to which two or more random variables move together.
During a study of two variables, if it has been observed that movement in one variable is reciprocated by an equivalent movement in the other variable in some way or another, then the variables are said to be correlated.
There are two types of correlation, namely, positive correlation and negative correlation. Variables are said to be positively or directly correlated when both variables move in the same direction.
Conversely, the correlation is negative or inverse when the two variables move in opposite directions.
The correlation value lies between -1 and +1, where a value close to +1 indicates a strong positive correlation, and a value close to -1 indicates a strong negative correlation. There are four correlation measures:
- Scatter diagrams
- Product-moment correlation coefficient
- Rank correlation coefficient
- Concurrent deviation coefficient
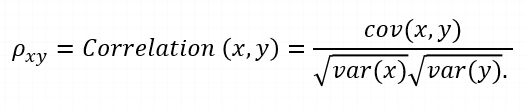
where,
var(X) = standard deviation of X
var(Y) = standard deviation of Y
Positive correlation occurs when two variables move in the same direction. When variables move in the opposite direction, they are said to be negatively correlated.
Types of Correlation
Correlation is of three types:
1. Simple Correlation: In simple correlation, a single number expresses the degree to which two variables are related.
2. Partial Correlation: When one variable’s effects are removed, the correlation between two variables is revealed in partial correlation.
3. Multiple correlation: A statistical technique that uses two or more variables to predict the value of one variable.
Covariance and Correlation Differences
1. The following points are noteworthy so far as the difference between covariance and correlation is concerned:
2. The measure used to indicate the degree to which two random variables change together is known as covariance.
3. The measure used to describe how strongly two random variables are related known as correlation.
Covariance is nothing but a measure of correlation. Conversely, correlation refers to a scaled form of covariance.
4. The correlation value occurs between -1 and +1. On the other hand, the covariance value lies between -∞ and + ∞.
5. Covariance is affected by changes in scale. If all values of one variable are multiplied by a constant and all values of other variables are multiplied by the same or different constants, then the covariance is changed. Against this, the correlation is not affected by changes in scale.
6. Correlation is dimensionless, i.e., a unit-independent measure of the relationship between variables. Unlike covariance, values are obtained by the product of the units of two variables.
Covariance and Correlation Comparison
Basis for comparison |
Covariance |
Correlation |
| Definition | Covariance is an indicator of the extent to which 2 random variables are dependent on each other. A higher number denotes higher dependency. | Correlation is a statistical measure that indicates how strongly two variables are related. |
| Values | The value of covariance lies in the range of -∞ and +∞. | Correlation is limited to values between the range -1 and +1 |
| Change in scale | Affects covariance | Does not affect the correlation |
| Unit-free measure | No | Yes |
Covariance and Correlation Similarities
Correlation and covariance are both measures used to quantify the relationship between two variables. Both measures are useful for understanding the relationship between variables, but they have some key differences.
One similarity between correlation and covariance is that they both measure only linear relationships between variables.
This means that when the correlation coefficient is zero, the covariance is also zero. Additionally, both correlation and covariance measures are unaffected by changes in location, which means that they are not affected by shifts in the data.
However, when it comes to choosing between covariance and correlation to measure the relationship between variables, correlation is often preferred over covariance.
One of the main reasons for this is that correlation is not affected by changes in scale, while covariance is. This means that when two variables are scaled differently, their covariance will change, but their correlation will remain the same.
Another reason why correlation is preferred over covariance is that correlation is always between -1 and 1, which makes it easy to interpret.
Covariance can be any real number, which can make it difficult to interpret the magnitude of the relationship.
