Cara Menyelesaikan Persamaan Eksponen

Tahukah kalian bagaimana cara menyelesaikan persamaan eksponen? Jika kalian belum tahu cara menyelesaikan persama eksponen, tenang saja karena kami akan berbagi bagaimana caranya untuk menyelesaikan persamaan eksponen. Maka dari itu alangkah baiknya anda membaca artikel berikut ini.

Penyelesaian Persamaan Eksponen

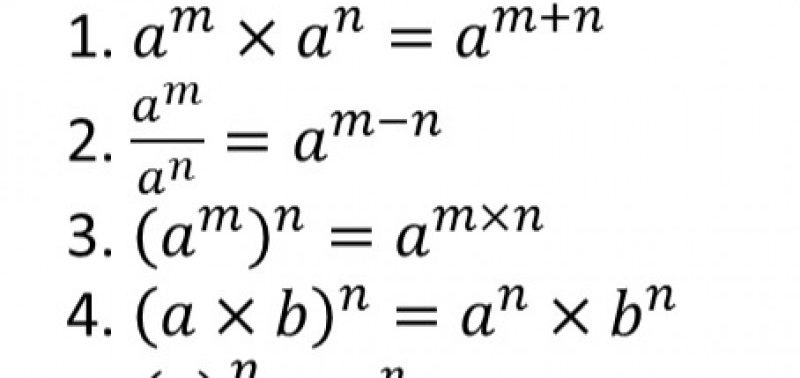
Penyelelesaian suatu persamaan eksponen dalam bentuk peubah X adalah semua nilai x yang memenuhi eskponen tersebut. Nilai nilai X yang menyebabkan persamaan eksponen menjadi bernilai benar. Berikut ini merupakan bentuk bentuk persamaan eksponen dengan sifat sifat yang dapat digunakan dalam menentukan solusinya.

A. Bentuk Persamaan a^f(x) = a^g(x)

Bentuk persamaan eksponen diatas memiliki bilangan pokok yang sama di kedua ruasnya yaitu a dan nilainya konstan. Akan tetapi pangkatnya memiliki nilai berbeda yaitu f(x) dan g(x). Agar kondisi persamaan tersebut bernilai benar adalah pada saat nilai pangkatnya sama yaitu saat f(x)=g(x).

Contoh Persamaan 

Tentukan penyelesaian dari 2^2x-7 = 8^1-x

Jawaban

Langkah awal yang harus dilakukan adalah dengan menyamakan bilangan pokok kedua ruas.

2^2x-7 = 8^1-x
2^2x-7 = (2³)^1-x
2^2x-7 = 2^3-3x

Karena bilangan pokoknya sudah sama maka dapat diperoleh sebagai berikut

2x – 7 = 3 – 3x
5x = 10
x = 2

Jadi penyelesaiannya yaitu x = 2

B. Bentuk Persamaan a^f(x) = b^f(x)

Bentuk persamaan eksponen ini memiliki bilangan pokok yang berbeda, yaitu a dan b, yang keduanya konstan. Akan tetapi kedua pangkatnya memiliki nilai yang sama yaitu f(x). Agar persamaan tersebut bernilai benar maka nilai f(x) harus sama dengan nol.

Contoh Persamaan

Tentukan penyelesaian dari 3^2x-2 = 5^x-1

Kedua bilangan pokok diatas berbeda dan tidak terdapat sifat pangkat yang bisa digunakan untuk menyamakan kedua bilangan pokok tersebut. Akan tetapi kedua pangkatnya bisa disamakan menjadi seperti berikut ini;

3^2x-2 = 5^x-1
3^2(x-1) = 5^x-1
9^x-1 = 5^x-1

Berdasarkan nilai pangkat yang sudah disamakan maka

x-1=0

x= 1

Jadi untuk penyelesain persamaan tersebut yaitu x=1

C. Bentuk Persamaan a^f(x) = b^g(x)

Persamaan eksponen ini memiliki bilangan pokok berbeda dan pangkat yang berbeda juga. Bilangan pokoknya yaitu a dan b serta pangkatnya yaitu f(x) dan g(x). Agar dapat menemukan solusi dari bentuk persamaan ini maka harus menggunakan logaritma.

Contoh Persamaan

Tentukan penyelesaian dari ($\frac{\mathrm{2/}}{}$)^x = 6^1-x

Bilangan pokok kedua persamaan berbeda dan juga bilangan pangkatnya berbeda. maka

log  ($\frac{\mathrm{2/}}{}$)^x = log 6^1-x
x log (2/3) = (1 – x) log 6       log aⁿ = n log a
x log (2/3) = log 6 – x log 6
x log (2/3) + x log 6 = log 6
x (log (2/3) + log 6) = log 6
x log 4 = log 6                    log a + log b = log (ab)
x = $\frac{log\mathrm{6/}}{log4}$
x = ⁴log 6

Jadi penyelesaiannya adalah x=⁴log 6

D. Bentuk Persamaan f(x)^g(x) = 1

Terdapat tiga macam kondisi yang menyebabkan persamaan ini dapat bernilai benar. yaitu

1. Karena 1^g(x) = 1 bernilai benar untuk setiap g(x), maka f(x)^g(x)=1 dapat bernilai benar jika f(x)=1
2. Karena (-1)^g(x) = 1 bernilai benar jika g(x) genap, maka f(x)^g(x) = 1 dapat bernilai benar jika f(x) = -1 dengan syarat g(x) bernilai genap.
3. Karena f(x)⁰ = 1 bernilai benar jika f(x) ≠ 0, maka f(x)^g(x) = 1 dapat bernilai benar jika g(x) = 0 dengan syarat f(x) ≠ 0.

Contoh Persamaan

Tentukan himpunan penyelesaian dari (2x + 3)^x-1 = 1

Jawaban

Cara Pertama

• f(x) = 1
• 2x+1 = 1
• 2x=2
• x=-1

Cara Kedua

• gx=0
• x-1=0
• x=1

Makah Himpunan penyelesaiannya adalah (-1,1)

Nah itulah pembahasan dan rangkuman terkait dengan cara menyelesaikan persamaan eksponen. Semoga pembahasan artikel kali ini dapat bermanfaat dengan baik untuk kalian.